But what is bias? According to the Oxford Dictionary it is “a strong feeling in favour of or against [...] one side in an argument, often not based on fair judgement”. The final part is what gives the word its negative connotation, although this is not a fair judgement in general. In simple terms, it is the expectation, more or less justified, that we have of what surrounds us. This expectation is what creates our intuition and conditions our imagination.

 

It is therefore our task to dwell on these two aspects and see to what extent Nature challenges them.

 

 

 

Despite this introduction, bias is one of the most interesting elements of evolution. Just as you don't have to be an expert in electrical engineering and semi-conductor materials to use a mobile phone or a computer, you don't have to be a student of Nature to experience it. In general, our basic actions and needs, such as hunger and thirst appear natural and indistinctive to us; if we want to move an arm, we do so, heedless of the complex network of electrical signals that triggered the contraction of our muscles, or the cellular bonds and interactions that make up their tissues. Come to think of it, if this were not the case, life would seem much more arduous. So we, unaware of the subtleties of the world, are delegated the task of living: this is where bias comes in. You don't need to be a student of gravity to know that if an apple comes off the tree it will fall, and it is taken for granted that anything that is left to 'fall' will in fact fall. This is a form of bias. Having no deep reason for what you see, you just assume that it is so and you start expecting that it will always be the case. Imagine how complicated any action would be if one doubted such simple things. Bias makes life simple, speeds it up and allows us to make considerations more quickly. It arises from our experiences and senses, shaping our expectations and giving rise to our intuition and imagination. As this is its nature, however, it often misleads us, limiting us to considering only what we know and can conceive, which as we shall see is considerably narrow.

 

 

Since bias arises from our experiences, which in everyday life are ultimately the result of our sensations, the most natural question is: are there phenomena which we cannot perceive with our sensations and which are therefore unimaginable for our brain? Wonderfully, yes. 

 

You might think as an example of the existence of viruses and bacteria, living beings so small that their existence would go unnoticed if there were no microscopes. However true this may be, it does not fully answer the question; in fact, discovering that there are living beings so small that they are not visible to the naked eye is, however not trivial, not a difficult concept to accept. It is conceivable, since it is like taking something that already exists and making it smaller. The crucial difference, however, is that we can actually see them with the right technology and so they fall outside the question. Are there things that, no matter how familiar their concept, are unimaginable?

 

A simple yet powerful example comes from the world of colours. Achromatopsia is a rare, sometimes congenital disease that eliminates the perception of colours. A person born with this disease is only sensitive to the intensity of light but not to its colours, seeing the world only in black and white. Not only has this person never seen a colour, but because he or she has never seen them, he or she cannot even imagine what they look like. On the contrary, there is evidence that animals such as bees see different colours than we do. Could you imagine a new colour?

 

A more mathematical example is the existence of an extra dimension. It is quite natural to know that we live in three dimensions: we can move left or right, forward or backward, and, jumping, up and down. All other directions are combinations of these three. If you were told that there is a fourth (spoiler: as there is), could you visualise it? 

 

For all these things, although the concept is clear, imagination already fails. Strange as it may seem, there are things on a higher level than this, and to see this it is necessary to enter the realm of modern physics.

 

 

What does it mean for a physicist to have 'understood' a phenomenon? Generally, it means having a mathematical model that allows numerical predictions to be made about experiments which then turn out to be correct. However, there is also another, more human way of 'understanding', which banally comes down to being able to imagine and in some way expect the result, numbers excluded. Below I would like to present two phenomena for which, while the 'mathematical understanding' is very clear, the other is quite different. To go into the depths of each would require an article each and that is beyond the scope of this article. However, while I ask you to take the phenomenon for granted, I would like you to focus on its peculiarity, without numbers. Don't worry if you don't understand, because even physicists can't say they really do if you exclude math. To paraphrase a former professor of mine, “you don't understand physics, you get used to it” (that is the whole point!), and from there comes a new insight to build future theories.

 

 

The first phenomenon comes from Einstein's theory of relativity. With the publication of Special Relativity (1905) and General Relativity (1915) something completely unexpected became apparent: the close link between space and time and their unification. Fascinating as the subject is and as rich in examples as it is, I will focus on one phenomenon in particular: time dilation. In simple terms, time does not flow in the same way everywhere and for everyone. As obvious as it may seem to us that a second spent for us is the same as a second spent for someone else, wherever that may be, it is false. 

 

We are not talking here about the feeling that time sometimes passes quickly when we are having fun or how it never passes when we are agitated, but about something objective and measurable. In fact, there is evidence that the passage of time is modified by the fact that either someone is moving at high speed or a different force of gravity is present. These effects are maximal for speeds close to the speed of light (~300,000 Km/s) or close to very heavy objects, where by 'heavy objects' we count multiple masses of the sun.

 

The basic concept is simple: gravity deforms time. To give a concrete example, time on the International Space Station runs faster than it does on Earth. This effect is so small that it goes almost unnoticed because of the lightness of the Earth, but if we were to take much heavier objects like Black Holes, the effects could be enormously bigger. 

 

Let's take an example: Alice and Bob are the same age and decide that Alice is going to spend the weekend near an object with a huge gravity, e.g. a fairly large black hole (how exotic!). In its most basic form, it means that if Alice and Bob, before separating, had taken two identical and synchronised clocks, they would have marked two different times when reunited. Let's exaggerate a little now in order to see some almost paradoxical consequences. Alice will relax for her 48 hours and then return to Bob, who will wait for her at home. After her nice, relaxing weekend, Alice returns home to discover something incredibly unusual: Bob has aged 48 years! They may start fighting over the misunderstanding but it’s useless, as Alice has really only spent 48 hours on holiday but Bob has really spent 48 years waiting for her to return. They are both right. It is indeed physically possible, although incredibly exaggerated here, that 1 hour in one place equals 1 year in another. You may have seen such a thing in the movie Interstellar (2014): that’s not just science-fiction but a real phenomenon. The example is extreme, but phenomena of this kind are measured and well established as real. Would you have ever guessed it?

 

 

If we have seen that unusual effects appear at high speeds or near incredibly heavy objects, even more bizarre things happen when you go into the microscopic world, on subatomic scales. The physics that studies these systems is the celebrated Quantum Mechanics. Among the most interesting and distinctive phenomena is one called 'superposition'. 

 

Let's imagine for a moment that the rules of the subatomic world also apply to ours and let us take a 'simple' example, for which my colleagues will excuse me some subtleties. We take a coin and toss it and expect it to come up heads or tails and indeed it does. But now let's make it more interesting: we want to make heads or tails come out while we are not looking at the coin. For this we simply take a small box, put the coin in it, shake it a bit and when we open the box we see if the coin shows heads or tails. We do this once, open the box and "heads"; again, "tails"; again "heads"; another time "heads"; and so on. Every time you open the box you always find heads or tails.

 

Ok, at this point, a physicist might be interested in finding some general rules that will allow him/her to predict the behaviour of the coin in the future if the experiment is repeated. For example, that it is 50% likely that the coin gives heads and 50% likely that it is tails. He/she will do the necessary math and will try to predict which result will come out before you open the box and check coin. He/she takes only one but fairly obvious key assumption, namely that even without looking inside the box, after shaking it, the coin is facing only heads or tails. Here is where the surprise comes: the accounts do not add up and do not reflect what you see from the result count. Desperate for such failure the physicist tries a different approach and assumes something extremely unusual in his/her model: that while in the box after being shaken, unseen, the coin is facing head and tails simultaneously. This is not to say that it is facing one of the two but you don’t know which one, but that it is really facing both of them the same time when we are not looking at it. Take a moment to reflect on this sentence, because if it doesn't bother you a little or seems natural to you, you might not have understood it (or if you did, please contact me!)! Definitely a crazy idea, but, even bigger surprise, after doing the calculations, the physicist finds that they match exactly what you see from your experiments. 

 

 

Do you see how unfair and limited our brains are? If we mixed red and yellow we would get orange, which we can imagine because we have seen it. But if I told you to mix the outcome of a coin toss, you would call me crazy, because such a thing has never been seen. And yet this is exactly what happens in experiments that are carried out on atoms or electrons. Although all physicists agree on the mathematics describing these phenomena, I think it is honest to say that there is no totally shared 'intuitive' interpretation of what is really going on. As some great physicists from N. Bohr to R. P. Feynman said: if you think you understand quantum mechanics, you don't understand quantum mechanics.

 

What can we conclude? In the quantum world, i.e. the very, very small world, our notion of 'reality' is blurred. Certain objects can have one property and its opposite simultaneously, without any paradoxes: this feature is called 'superposition' and its existence, at the expense of interpretation, is now an established fact. Can you imagine something like this?

 

 

The phenomenon of 'superposition' is already symbolic of that category of unimaginable and non-intuitive phenomena. Moreover, since such phenomena are 'small', they are impossible to see. The phenomena that a high-energy physicist studies go either on even smaller scales and in a regime where the studied objects go even faster and all the previous effects are mixed. Unlike the way in which, for example, a doctor sees a bacterium, a physicist can never see the phenomena he studies in their true essence (whatever that means); so how can one do physics and move on? 

 

The answer has in fact already been given: it is not necessary to understand something in its essence in order to be used and studied. Even a person who only sees in black and white can learn that the sky is 'blue' and a meadow 'green', although it will be impossible to get the true feeling of what that means.  One could also be inclined to think that all meadows will be green, and will occasionally be wrong if the catalogue of those unseen colours is not refined. This has a nostalgic feel to it, but it is what we have.

 

 

At this point you might ask yourself: OK with colours it seems feasible, but how to develop the same thing for such complex and mysterious phenomena as time dilation, superposition and so on? The answer is as simple as it is puzzling: mathematics. Where our intuition fails, a physicist follows mathematics and, following its rules, arrives at the answer and tries to make physical sense of it.

 

This confidence game is all the more extraordinary when you think of the results it has brought.  In the extraordinary little book that is E. Wigner’s “The Unreasonable Effectiveness of Mathematics in the Natural Sciences”, Wigner opens the reflection on how a tool created by an all-too-limited mind like ours that cannot imagine most of our world, mathematics, is able to go beyond our evolutionary limits and lead us to develop a new intuition, entirely based on mathematics and the numbers that come out of our experiments. Certain mathematical systems have been created to describe a phenomenon, and it turns out that they contain many more that we never imagined existed and were not dealing with! The amazement then culminates in the realisation that these 'educated guesses' dictated solely by mathematics turn out to be correct.

 

 

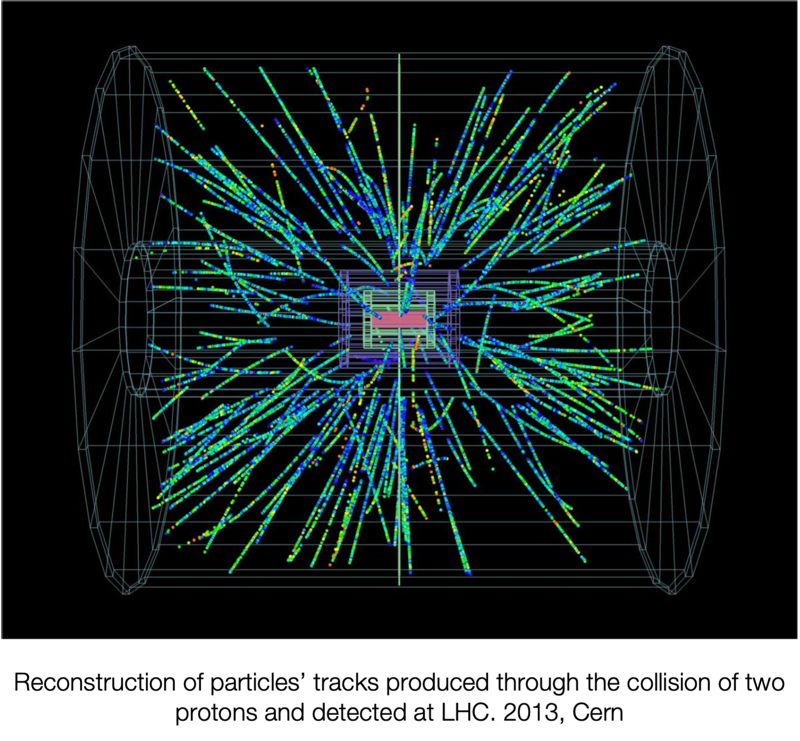
Mathematical foresight of this kind is demonstrated in various experiments, of which the most striking in recent years are probably two. The first concerns the discovery of the Higgs Boson in 2012, whose existence was taken for granted by theoretical physicists. Why? How could they be so sure that this particle existed? “Just” mathematical consistency. Put simply, what we can basically calculate of these phenomena is only probability, which mathematically is defined as a number between 0 and 1: 0 indicates an impossible event and 1 a certain one; any number outside this range cannot be interpreted as probability. If a particle like the Higgs had not existed, the model would have produced probabilities outside the range and therefore the result would have been mathematically inconsistent with the model itself. Of course changing the whole model was also an option, but if we choose the path that seems simplest, i.e. just adding an extra piece (and this is also a form of bias), it led straight to its existence. Its discovery, like that of so many other particles theorised before their discovery in the same way, is one of the great achievements of theoretical physics.

 

The second example concerns the confirmation of the existence of black holes. Theorised by Karl Schwarzschild in 1916 through the newly born General Relativity, Schwarzschild discovered that the theory made possible the existence of objects so heavy that not even light could escape. Despite much speculation over the past century, the black hole was proved to be something inevitable in the theory, and finally in 2019 the first picture of one such object was taken by the Event Horizon Telescope. It was a stunning success of technology and theory.

 

 

 

Having said that, let's try to get down to business in the work of a particle physicist and see how these 'limitations come in'. I said earlier that the Higgs Boson is a 'particle', but what is a particle? This is where things already start to get hazy. In the late nineteenth early twentieth century, people began to imagine them as little balls moving around and interacting with each other to create the world we see. This is in fact the way most physicists still imagine them, even though they know it is not the truth. As technology and theory progressed, it was soon realised that these objects, obeying Quantum phenomena such as those described above, could not be thought of as such; the main reason is that 'strange' properties such as ‘superposition’, which definitely do not suit a ‘little ball', began to characterise the very concept of a particle as we understand it today and, eventually, the analogy became meaningless. 

 

So what are they to a physicist? The answer is somewhat disappointing and obvious in the light of what we have been saying: being in fact something totally different from anything we can intuitively know, it is defined only in mathematical terms. Without going into detail, it is defined as an entity that possesses certain measurable properties that do not change in space or time, i.e. wherever and whenever we want to measure them. For the sake of concreteness of these properties for example is its mass, i.e. roughly speaking its weight. The definition may sound strange, but in the end it is not so bad. If I told you that a car is an object that has four wheels no matter where it is, it would be clear: no matter whether you see it on the road, in the mountains or at the seaside, it will still have four wheels and you know it will still be a car. You might object to me that there are other objects with four wheels that are not cars, and indeed so even particles have more properties needed to distinguish them unambiguously. As you can see, this definition is also in fact similar to working with an unknown colour: you know it exists, you know it has certain properties, but getting an intuition of them is very hard if not impossible.

 

Physicists in the last century have discovered many particles, all with different properties, and one branch of physics has taken it upon itself to study how these interact: particle physics. Don't be frightened by the what could seems “the mysterious and obscure concept of ‘particle’” and the various types that one encounters. In a way it is like telling you that there is something called a “plant” and that there are many types, and that is why there is someone who studies them and a discipline called ‘botany'. 

 

 

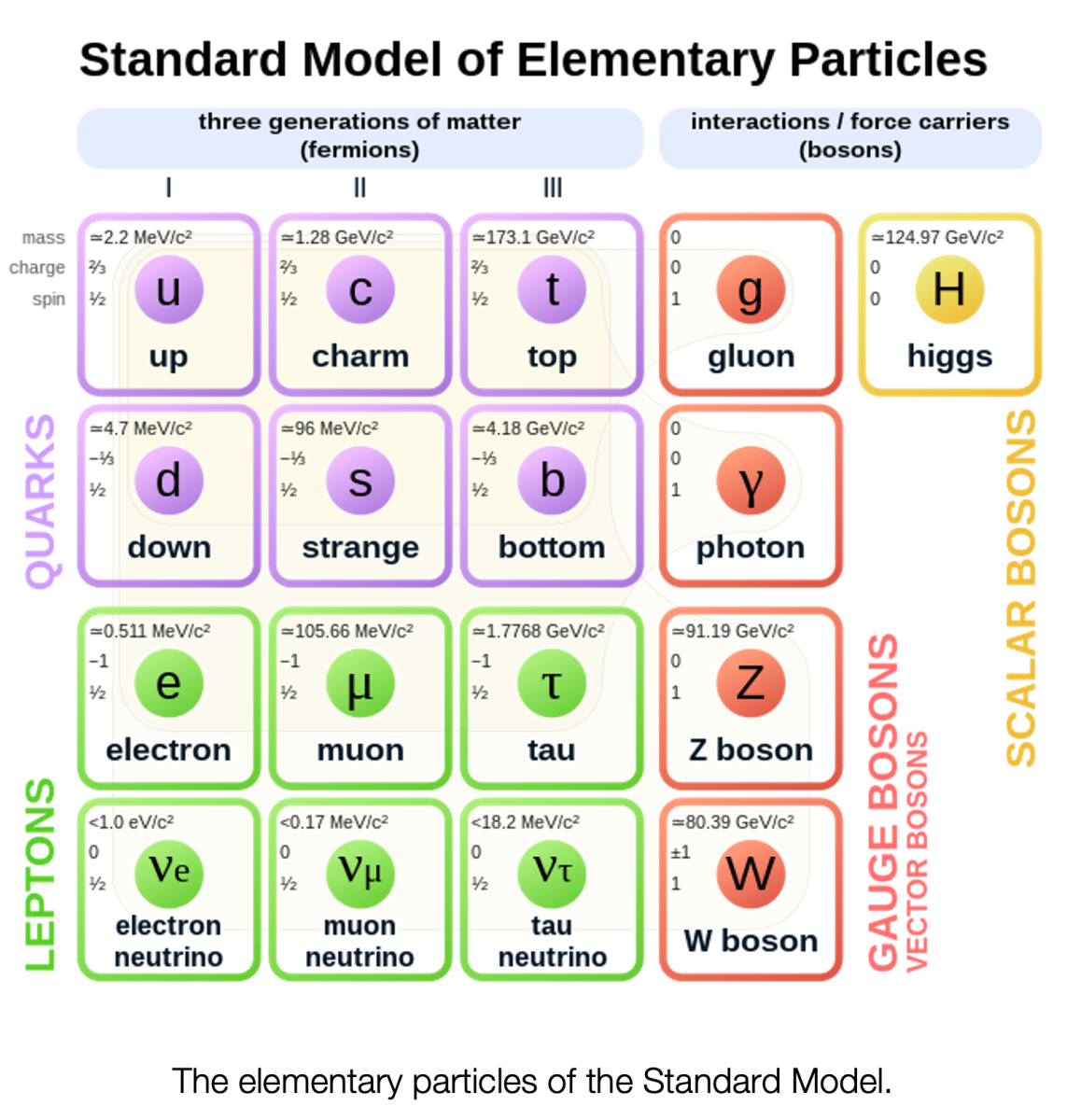
We can have for example a particle that disappears and produces another couple of different ones and we physicists ask ourselves: which ones can it produce? How often does this happen? How long does it take before it happens? And so on and so forth. Over time we have catalogued many of them until we have found 17 types (sorting by masses) that seem special compared to the others and that we call "elementary particles", that is, those that we think are the constituents of all the others and that are not themselves composed of other smaller ones. All our current knowledge is encapsulated in a model we call the Standard Model. The achievements with it are extraordinary given the precision with which its predictions have been verified, and only in recent years have we begun to see significant discrepancies in various experiments.

 

 

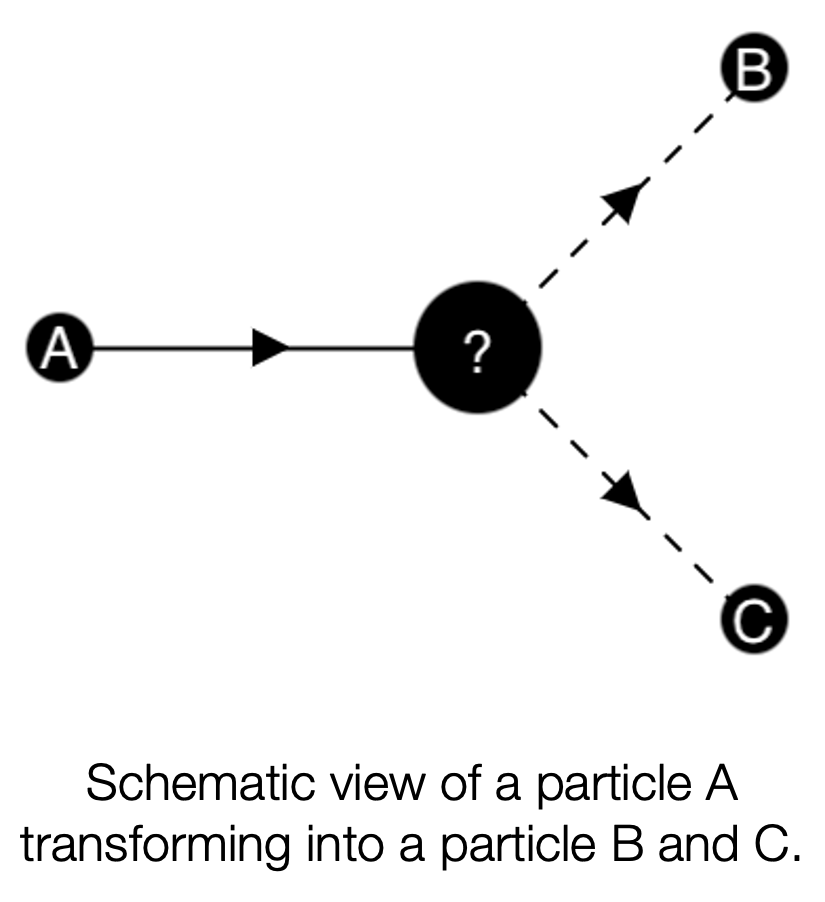
How do we know if what we think about them, or rather our mathematical model, is correct? This is where the 

'confidence' part comes in: we perform experiments, we make these particles interact with something we know, which we call a 'detector', 

and we observe the effects; these are compared with the predictions and if they match EUREKA! For example, I might predict that a certain particle A will turn into a particle B and C 90% of the time: if they don't, it's not the right model. Interestingly, we can only see the 

end result, but not everything else: a particle enters (A), does things we cannot see and when it interacts with our instrument we see the consequences on which we base our knowledge (appearance of B and C). Not all particles interact equally with each other: some as soon as they meet the detector they immediately leave a trace of their passage or even stop, others are affected so little that they pass through and leave almost no trace of their passage. For example, among these, some called “neutrinos" are the most elusive: they interact so little with the other particles that they even manage to cross the whole Earth almost undisturbed! Yet there are so many of them that about 60 billion neutrinos per square centimeter pass through every second!

 

 

To say that we understand how Nature works is to trust mathematics and interpret it to understand what happens in the meantime, when we can only see the final effects!

 

 

 

The world despite being 'user-friendly' is incredibly complex, unimaginable and deeply counterintuitive at its roots. Mathematics and the numerical results of experiments provide us with a way to explore this unknown land. This is part of the fascination of this subject. We do not know what mysteries await us. We know that the Standard Model is not complete, but we do not yet know how to complete it. Until now, Nature has always shown itself to be more than we expected, and it may be the case that it will do so again. Only those who are ready to let go of all bias and are open to accepting the true essence of Nature will be able to enter this new and unexplored world. Lasciate ogne bias, voi ch’intrate!

 

-‌‌Arturo de Giorgi